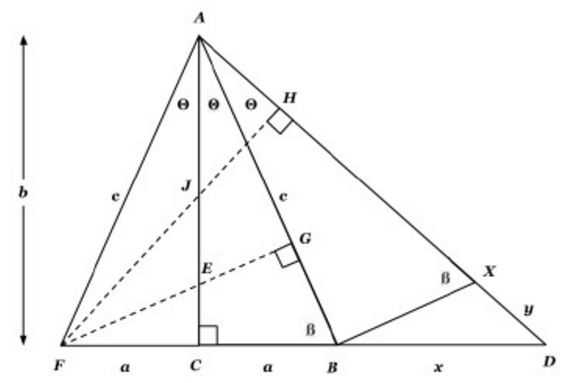
Equation (2) will become $\cos (\theta \theta) = \cos \theta \, \cos \theta \sin \theta \, \sin \theta$ $\cos 2\theta = \cos^2 \theta \sin^2 \theta$ → Equation (4) The Pythagorean Identity sin 2 θ cos 2 θ = 1 can be taken as sin 2 θ = 1 cos 2 θ and Equation (4) will become $\cos 2\theta = \cos^2 \theta (1Basic Trigonometric Formula and Identities (1) sinθ s i n θ cosecθ c o s e c θ = 1 (2) cosθ c o s θ secθ s e c θ = 1 (3) tanθ t a n θ cotθ c o t θ = 1Trigonometric identities A Complete List of Identities in Trigonometry Sec 2 θ = 1 Tan 2 θ Tan 2 θ = Sec 2 θ 1 Csc 2 θ Cot 2 θ = 1 given in the question as mathematical equation using trigonometric ratios correctly, 90% of the work will be over

Trigonometry Reciprocal Identities Expii
Trigonometric identities tan 2 theta formula
Trigonometric identities tan 2 theta formula-Trigonometric Identities ( Math Trig Identities) sin (theta) = a / c csc (theta) = 1 / sin (theta) = c / a cos (theta) = b / c sec (theta) = 1 / cos (theta) = c / b tan (theta) = sin (theta) / cos (theta) = a / b cot (theta) = 1/ tan (theta) = b / a sin (x) = sin (x) · As below Quotient Identities There are two quotient identities that can be used in right triangle trigonometry A quotient identity defines the relations for tangent and cotangent in terms of sine and cosine Remember that the difference between an equation and an identity is that an identity will be true for ALL values


Much From Little
Identities expressing trig functions in terms of their supplements Sum, difference, and double angle formulas for tangent The half angle formulas The ones for sine and cosine take the positive or negative square root depending on the quadrant of the angle θ/2 For example, if θ/2 is an acute angle, then the positive root would be used1803 · sin 2 ( 3 x 4 − 5 x 2 87) cos 2 ( 3 x 4 − 5 x 2 87) = 1 sin 2 ( 3 x 4 − 5 x 2 87) cos 2 ( 3 x 4 − 5 x 2 87) = 1 tan2(θ)1 = tan 2 ( θ) 1 = Show Solution tan 2 ( θ) 1 = sec 2 ( θ) tan 2 ( θ) 1 = sec 2 ( θ) If you know the formula from Problem 1 inCosec(2nπ θ) = cosecθ;
Tan ( α − β) = tan ( α) − tan ( β) 1 tan ( α) tan ( β) \tan (\alpha \beta) = \dfrac {\tan (\alpha) \tan (\beta)} {1 \tan (\alpha) \tan (\beta)} tan(α−β)= 1tan(α)tan(β)tan(α)−tan(β) By the way, in the above identities, the angles are denoted by Greek lettersLHS = 1 sin θ cos θ = ( 1 sin θ) cos θ) × ( 1 − sin θ) 1 − sin θ = 1 − sin 2 θ cos θ ( 1 − sin θ) = cos 2 θ cos θ ( 1 − sin θ) = cos θ ( 1 − sin θ) = RHS Restrictions undefined where cos θ = 0, sin θ = 1 and where tan θ is undefined Therefore θ ≠ 90 °;0117 · Trigonometric equations can be solved using the algebraic methods and trigonometric identities and values discussed in earlier sections Solve the equation 2 cos θ − 1 = 0 for 0 ≤ (tan 2 theta)`, so we have `tan 2 theta1/(tan 2 theta)=0` `tan^2 2θ = 1`
Cos(2nπ θ) = cosθ;Cos 2 θ sin 2 θ = 1 {\displaystyle \cos ^ {2}\theta \sin ^ {2}\theta =1} The other trigonometric functions can be found along the unit circle as tan θ = y B {\displaystyle \tan \theta =y_ {\mathrm {B} }\quad } and cot θ = x C , {\displaystyle \quad \cot \theta =x_ {\mathrm {C} },}All the trigonometric identities on one page Color coded Mobile friendly With PDF and JPG downloads



How Do You Simplify 1 Tan 2 X 1 Tan 2 X Socratic



Revision Trigonometry Siyavula
Then multiplying the numerator and denominator inside the square root by (1 cos θ) and using Pythagorean identities leads to tan θ 2 = sin θ 1 cos θ {\displaystyle \tan {\frac {\theta }{2}}={\frac {\sin \theta }{1\cos \theta }}}This trigonometry video tutorial explains how to use the sum and difference identities / formulas to evaluate sine, cosine, and tangent functions that have aSec(2nπ θ) = secθ;



Show 1 Tan 2theta 1 Sintheta 1 Sintheta 1



Double Angle Identities Trigonometry Socratic
Identities 1) Periodicity Identities sin(2nπ θ) = sinθ;Cosec 2 a = 1 cot 2 a; · In trigonometry formulas, we will learn all the basic formulas based on trigonometry ratios (sin,cos, tan) and identities as per Class 10, 11 and 12 syllabi Also, find the downloadable PDF of trigonometric formulas at BYJU'S


Trigonometry Identities



Art Of Problem Solving
1109 · Periodicity Identities Sine, cosine, secant and cosecant have periods 360 ∘ ( 2 π) while tangent and cotangent have periods 180 ∘ ( π) sin ( θ 360 ∘) = sin 0918 · In this post, we are providing you with the Trigonometry notes useful for the examinations It will help you memorize basic formulas of Trigonometry Important Trigonometric Ratio Identities In order to get hold of the basic concepts of trigonometry, you must learn all the important trigonometric ratio and their identities Trigonometric RatiosSiyavula's open Mathematics Grade 11 textbook, chapter 6 on Trigonometry covering Reduction formula



2sinxcosx Identity Gamers Smart



Trigonometric Identities A Plus Topper
· Trigonometry Formulas for class 11 play a crucial role in solving any problem related to this chapter Also, check Trigonometry For Class 11 where students can learn notes, as per the CBSE syllabus and prepare for the exam List of Class 11 Trigonometry Formulas Here is the list of formulas for Class 11 students as per the NCERT curriculum · Hence, we've also verified the three powerreducing formulas using the three halfangle identities Example 2 Apply the appropriate power reduction identity to rewrite $\sin^4 \theta$ in terms of $\sin \theta$ and $\cos \theta$ (and both must only have the first power) · x = −2 ± √22 − 4 × tanθ ×(− tanθ) 2tanθ x = −2 ± √4 4tan2θ 2tanθ or x = −2 ± 2√sec2θ 2tanθ or x = −2 ± 2secθ 2tanθ



Trig Integrals Trig Substitution



32 Prove The Trigonometric Identity Sec 6 Theta Tan 6 Theta 3 Tan 2 Theta Sec 2 Theta If Sec Theta Tan Theta P Find The Value Of Csc Theta
The trigonometric power reduction identities allow us to rewrite expressions involving trigonometric terms with trigonometric terms of smaller powers This becomes important in several applications such as integrating powers of trigonometric expressions in calculus Using the power reduction formulas, we can derive the following halfangle formulasFree trigonometric identity calculator verify trigonometric identities stepbystep This website uses cookies to ensure you get the best experience By · √a 2 x 2 x = a tan θ 1 – tan 2 θ = sec 2 θ √x 2 − a 2 x = a sec θ sec 2 θ – 1 = tan 2 θ



Solved Find The Value Of Tan 2 Theta If Theta Is In The Chegg Com



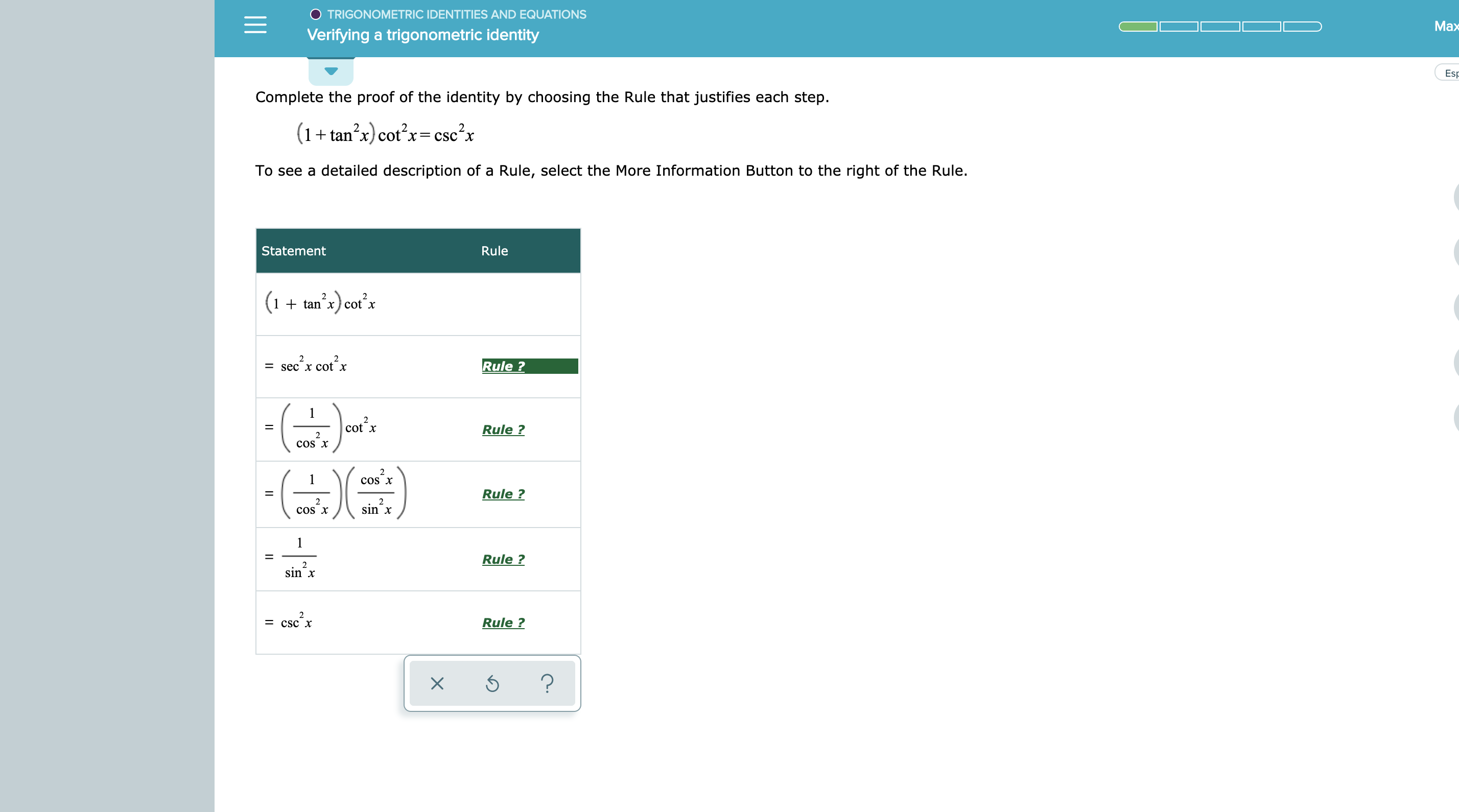
Solved Establish The Identity 1 Tan 2 Theta 1 Tan 2 Chegg Com
SubsectionUsing Trigonometric Ratios in Identities 🔗 Because the identity 2x2 − x − 1 = (2x 1)(x − 1) 🔗 is true for any value of x, it is true when x is replaced, for instance, by cosθ This gives us a new identity 2cos2θ − cosθ − 1 = (2cosθ 1)(cosθ − 1) 🔗Cot(2nπ θ) = cotθ;Using basic trig identities, we know tan(θ) can be converted to sin(θ)/ cos(θ), which makes everything sines and cosines Now work out the left side of the equation $$2sin^2(θ) = 2sin^2(θ)$$ The two sides are identical, so the identity has been verified!



Much From Little



Trouble Applying The Tan Double Angle Formula For 5 Tan 2 Theta 4 Cot Theta Mathematics Stack Exchange
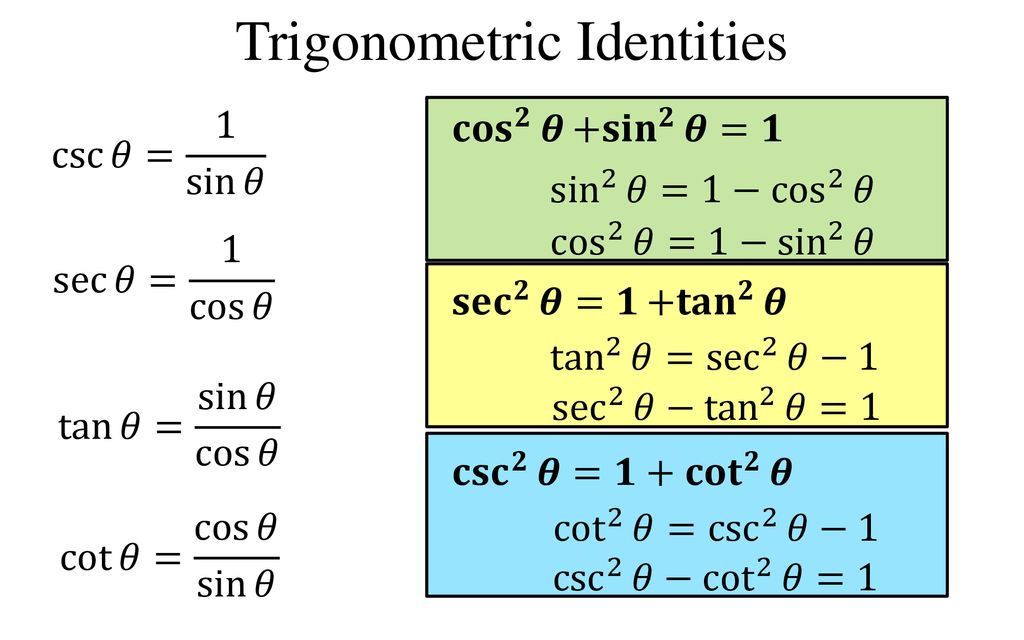
05 · A trigonometric equation is written as P1 (sin θ, cos θ, tan θ, cot θ, sec θ, cosec θ) = P2 (sin θ, cos θ, tan θ, cot θ, sec θ, cosec θ), where P1 and P2 are rational functions A trigonometric equation which is always true and holds good for every angle is called a trigonometric identity Steps to solve a trigonometric equation areHalf angle formulas can be derived from the double angle formulas, particularly, the cosine of double angle For easy reference, the cosines of double angle are listed below cos 2θ = 1 2sin2 θ → Equation (1) cos 2θ = 2cos2 θ 1 → Equation (2) Note that the equations above are identities, meaning, the equations are true for any value of the variable θFormula $\sec^2{\theta}\tan^2{\theta} \,=\, 1$ The subtraction of square of tan function from square of secant function equals to one is called the Pythagorean identity of secant and tangent


Pythagorean Identities Mathbitsnotebook Ccss Math


Solving Trigonometric Equations With Identities Precalculus
· Trigonometric functions with Formulas What are Trigonometric derivatives Heights and distance Trigonometry formula Involving Sum Difference Product Identities Pythagorean Theorem Differentiation Formula Basic Trig Identities;1tan2 A = sec2 A Somecommonlyneededtrigonometricidentities Example Suppose we wish to find Z π 0 sin2 xdx The strategy is to use a trigonometric identity to rewrite the integrand in an alternative form which does not include powers of sinx The trigonometric identity we shall use here is one of the 'double angle' formulae cos2A = 1−2sin2 A By rearranging this we can write sin2 A = 1 21 sin 2 θ is the commonly used notation for (sin θ) 2, likewise for other trigonometric ratios 2 sec 2 θ tan 2 θ = 1 is meaningless when θ = 90 ° But still it is an identity and true for all values of θ for which sec θ and tan θ are defined Thus, an identity is an equation that is true for all values of its domain values 3



What Is The Value Of Sin 2theta 1 1 Tan 2theta



Power Reducing Formulas And How To Use Them With Examples Owlcation
2) Trigonometric Identities sin2θcos2θ=1 ⇒ sin 2 x = 1 – cos 2 x ⇒ sin x = √(1 – cos 2 x)Trigonometric Cofunction Identities and Formulas, cofunction identities, cofunction calculator, cofunction identity, cofunction identities examplesIn simple language trigonometry can be defined as that branch of algebra, which is concerned with the triangle



Tangent Half Angle Formula Wikipedia


5 1 Fundamental Trig Identities Sin 1cos 1tan 1 Csc Sec Cot Csc 1sec 1cot 1 Sin Cos Ppt Download
Introduction This is a continuation of the first blog on Trigonometric Identities, we recommend you to read that first To visit that please click here Trigonometric Identities Part 1 Most of us find it difficult to understand Trigonometry as it's hard to remember so many related formulae270 ° Show AnswerTan(2nπ θ) = tanθ;



Prove The Identity Sin 2 Theta 2 Tan Theta Sin Theta 2tan Theta Study Com


Trigonometric Identities
Basic Trigonometry Formulas There are basically 6 ratios used for finding the elements in Trigonometry sine, cosine, tangent, cotangent, cosecant, and secant are called Trigonometric Functions that defines the relationship between the sides and angles of the triangleFollowing table gives the double angle identities which can be used while solving the equations You can also have sin2θ,cos2θ expressed in terms of tanθ as under sin2θ =2 The Elementary Identities Let (x;y) be the point on the unit circle centered at (0;0) that determines the angletrad Recall that the de nitions of the trigonometric functions for this angle are sint = y tant = y x sect = 1 y cost = x cott = x y csct = 1 x These de nitions readily establish the rst of the elementary or fundamental identities given in the table below


Trigonometry Identities



Double Angle Formulas Trigonometry Teachoo 2x 3x Formula Provi
Let θ = A = B;Ratio Identities Tan θ = Sin θ/Cos Trigonometric Identities Formula Similarly, an equation which involves trigonometric ratios of an angle represents a trigonometric identity The upcoming discussion covers the fundamental trigonometric identities andUsing Trig Identities to Solve a Quadratic in Sin x Category Mathematics In the first of this pair of Casio videos, the identity sin 2 x cos 2 x≡ 1 is used to solve fully the equation 9sin 2 x 21sinx = 3cos 2 x 12 The second video explores how a graphical calculator can be used to find solutions of the equation by plotting both sides of the equation we are trying to solve, and
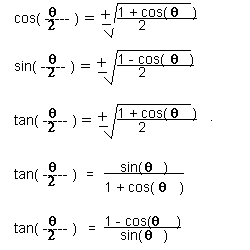


Double And Half Angle Formulas



Trigonometry Reciprocal Identities Expii
1107 · tan(2π−θ) = tanθ;Proving a trigonometric identity refers to showing that the identity is always true, no matter what value of x x x or θ \theta θ is used Because it has to hold true for all values of x x x, we cannot simply substitute in a few values of x x x to "show" that they are equal It is possible that both sides are equal at several values (namely when we solve the equation), and we might falsely
x-1=sec(squared)x.jpg)


10 Identity Tan Squared X 1 Sec Squared X Trigonometry Educator Com


Trigonometric Identities And Equations Ppt Download


Answered Trigonometric Identities And Equations Bartleby



Show That The Following Are Not Trigonometric Identities 1 Tan 2x 2tan X 2 Sec X Sqrt 1 Tan 2 X 3 Sin X Y Sin X Sin Y Study Com
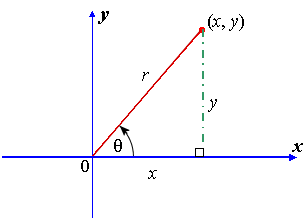


1 Trigonometric Identities


Ilectureonline
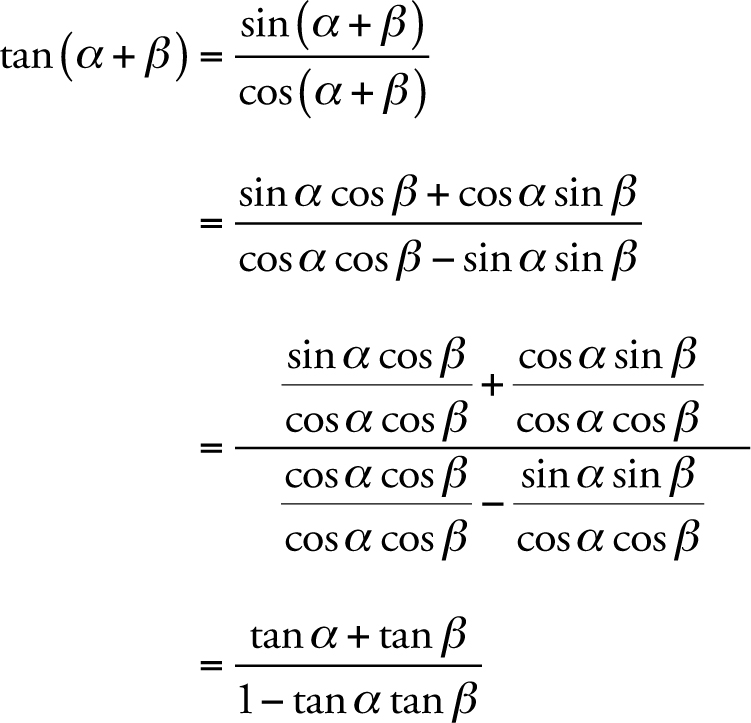


Tangent Identities


Derivatives Of Trigonometric Functions



Rd Sharma Solutions For Class 10 Chapter 6 Trigonometric Identities Exercise 6 1 Get Pdf



How Do You Verify The Identity Tan2theta 2 Cottheta Tantheta Socratic



Precalculus Trigonometry Trig Identities 29 Of 57 Formula For Lowering Power Tan 2 X Youtube



Analytic Trigonometry



14 2 Trigonometric Identities
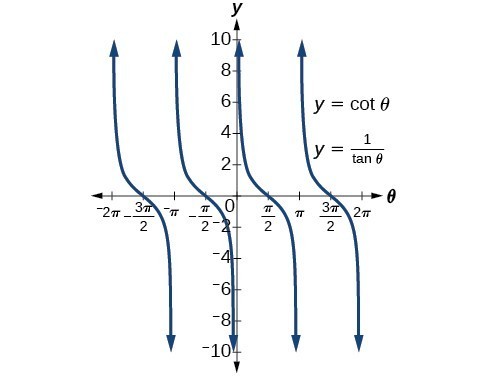


Solving Trigonometric Equations With Identities Precalculus Ii
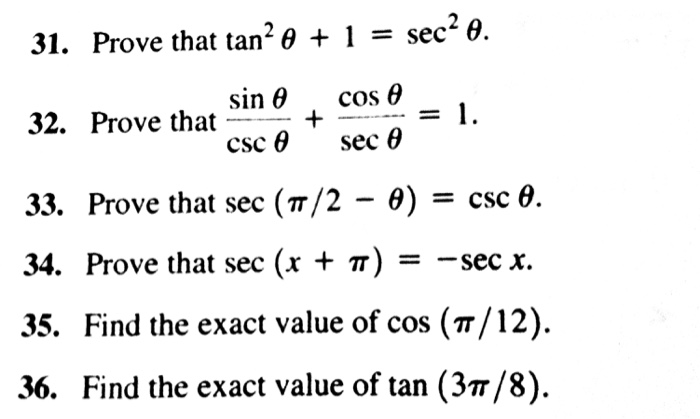


Solved 31 Prove That Tan 2 Theta 1 Sec 2 Theta 32 Chegg Com



Trigonometrical Ratios Or Functions A Plus Topper


What Is The Formula Of Tan2x Quora



Summary Of Trigonometric Identities
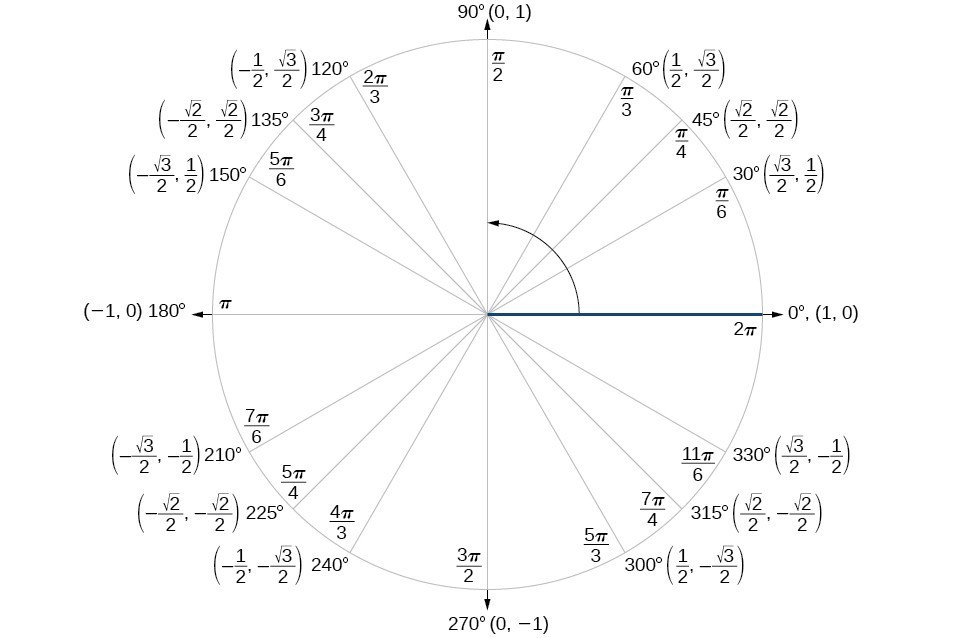


Sum And Difference Identities Precalculus Ii


The Unit Circle And Trigonometric Identities Crystal Clear Mathematics



Sec 6x Tan 6x 1 2 Tan 2x Sec 2x Important Difficult Trigonometric Identity Youtube



The Reciprocal Trigonometric Functions Problem 3 Trigonometry Video By Brightstorm



Verifying A Trigonometric Identity Tan 2 X 1 Sec X Sec X Youtube


What Is The Formula Of Tan2x Quora
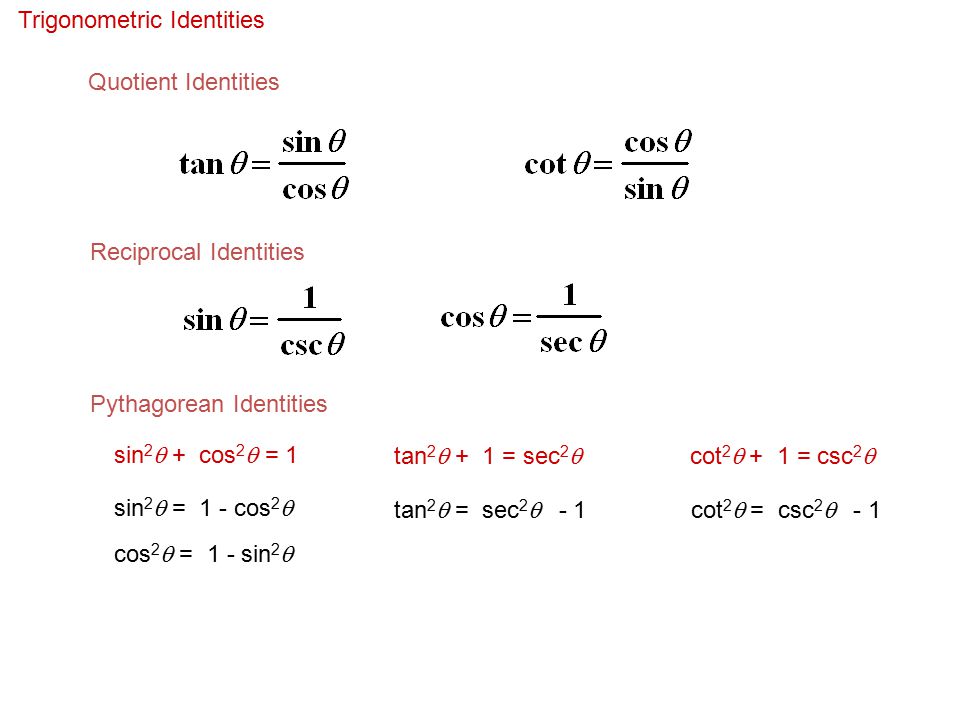


11 Basic Trigonometric Identities An Identity Is An Equation That Is True For All Defined Values Of A Variable We Are Going To Use The Identities To Ppt Download



How Does The Trigonometric Identity 1 Cot 2 Theta Csc 2 Theta Derive From The Identity Sin 2 Theta Cos 2 Theta 1 Mathematics Stack Exchange



Trigonometric Identities Topics In Trigonometry



Trigonometric Identities



Get Answer Prove The Given Identity Cos 2 Theta 1 Tan2 Theta 1 Which Transtutors



List Of Trigonometric Identities Wikipedia
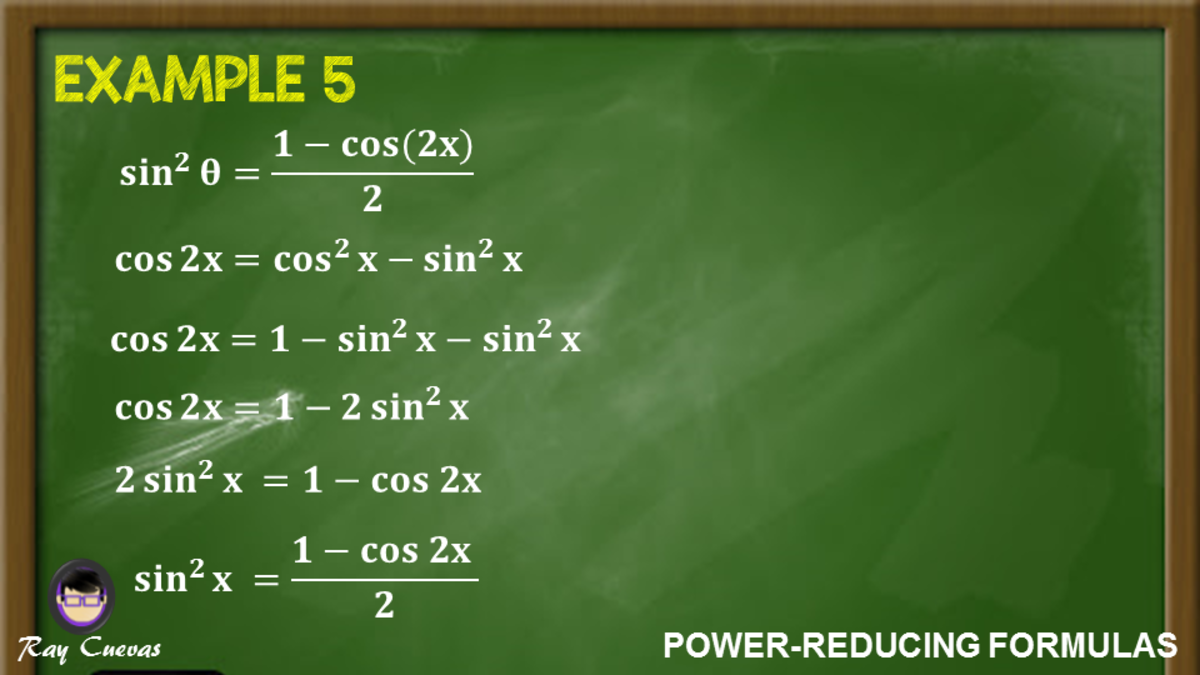


Power Reducing Formulas And How To Use Them With Examples Owlcation


What Are The Quotient Identities For A Trigonometric Functions Socratic



Trigonometric Identities List Of Trigonometric Identities Examples
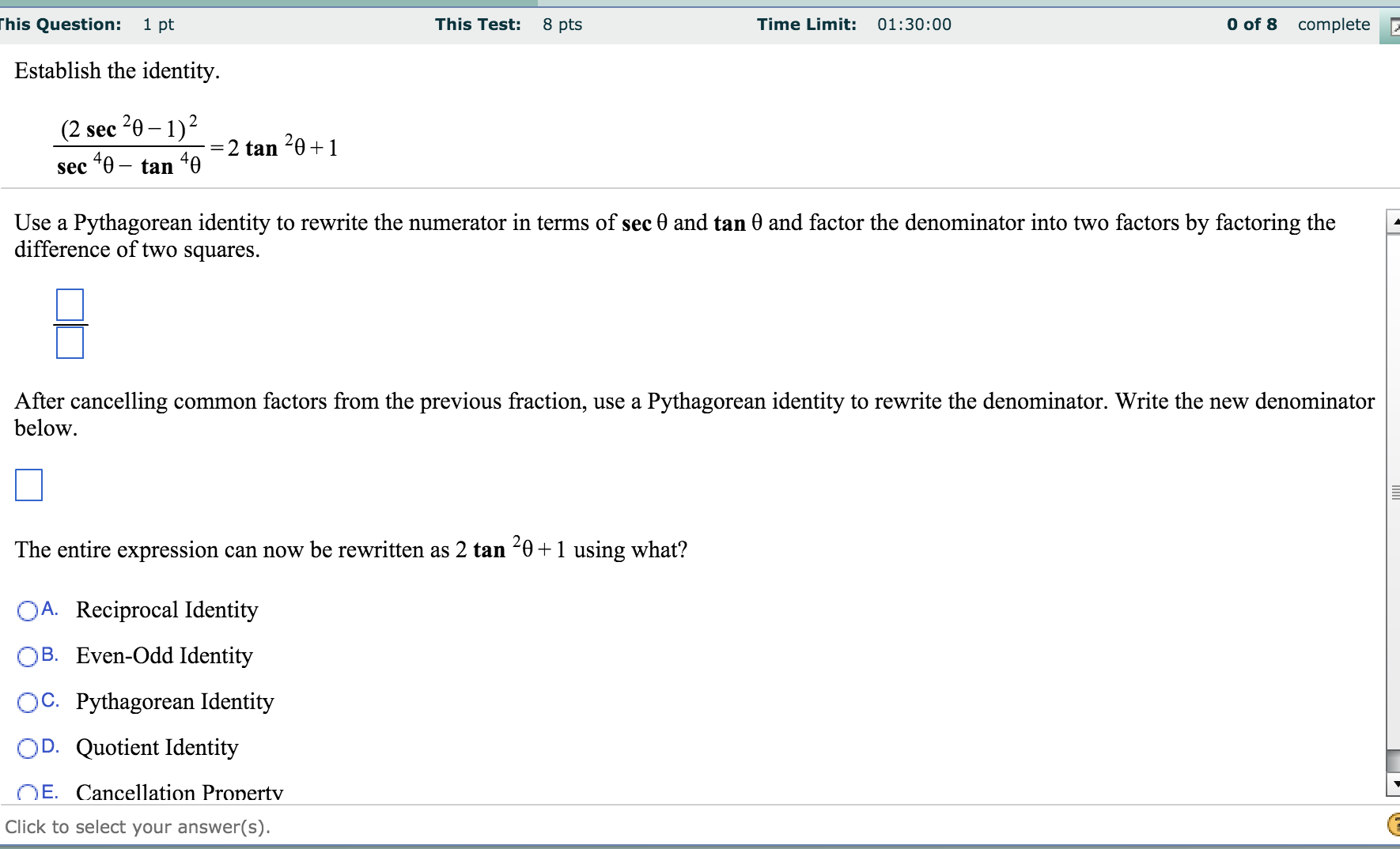


Solved Establish The Identity 2 Sec 2 Theta 1 2 Se Chegg Com



Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube


How I Remember Trig Identities Part 2 Beyond Solutions



Trigonometry Learning Commons



Proof Tan 2 1 Sec 2 Youtube



Rd Sharma Solutions For Class 10 Chapter 6 Trigonometric Identities Exercise 6 1 Get Pdf


Trigonometric Identities Topics In Trigonometry



Summary Of Trigonometric Identities
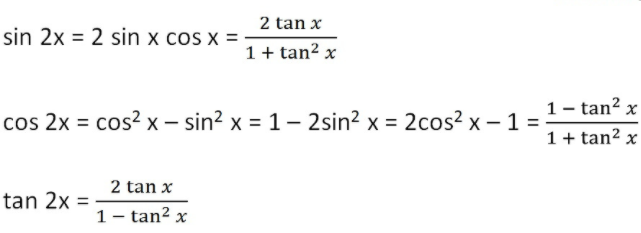


Formula Of Trigonometry Sin Cos Tan Cot Sec Cosec



Warm Up Prove Sin 2 X Cos 2 X 1 This Is One Of 3 Pythagorean Identities That We Will Be Using In Ch 11 The Other 2 Are 1 Tan 2 X Sec 2 X Ppt Download



14 2 Trigonometric Identities



How Do You Prove The Identities Cosx Secx Sinx Cscx Sec 2x Tan 2x Socratic



How To Use Double Angle Identities Studypug



Summary Of Trigonometric Identities


The Trigonometric Ratios Of Angl



Solved Establish The Identity Tan 12 Theta 3 Tan 4 Chegg Com



2sinxcosx Identity Gamers Smart



Precalculus Trigonometry Trig Identities 47 Of 57 Solve Tan 2 Theta 4 0 Theta Youtube


Cochranmath Solving Trigonometric Equations


Complex And Trigonometric Identities Introduction To Digital Filters



Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo
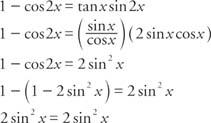


Double Angle And Half Angle Identities


What Is The Formula Of Tan2x Quora



Ppt Warm Up Powerpoint Presentation Free Download Id


Prove That Math Tan 2 Theta 1 Sec 2 Theta Math Quora
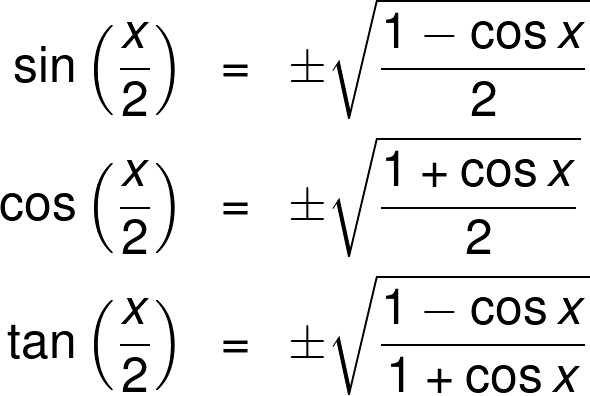


Half Angle Calculator


The Trigonometric Ratios Of Angl
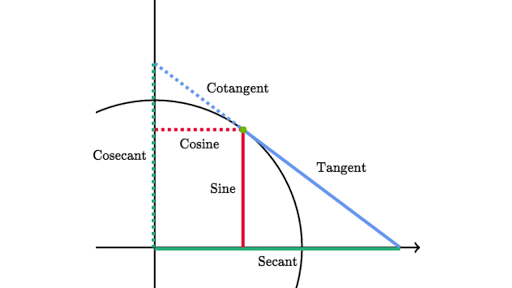


Trig Identity Reference Article Khan Academy



Trigonometric Identities A Plus Topper



Powers Of Trigonometric Functions



Trigonometric Identities Simplify Expressions Video Lessons Examples And Solutions
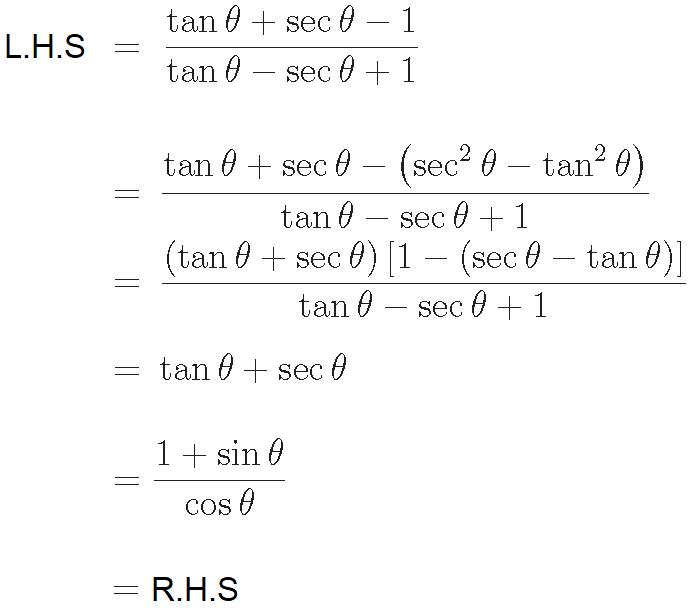


Basic Trigonometric Identities


Ilectureonline



Integrate Tan 2x
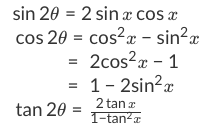


How To Use Double Angle Identities Studypug
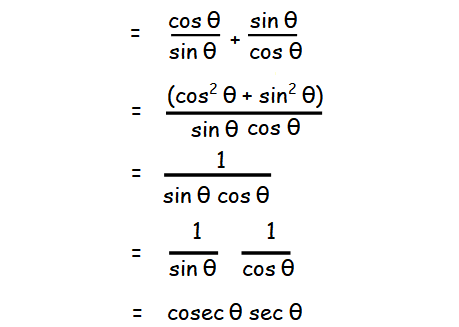


Proving Trigonometric Identities



Tangent Half Angle Formula Wikipedia



Integrate Cosec 2x
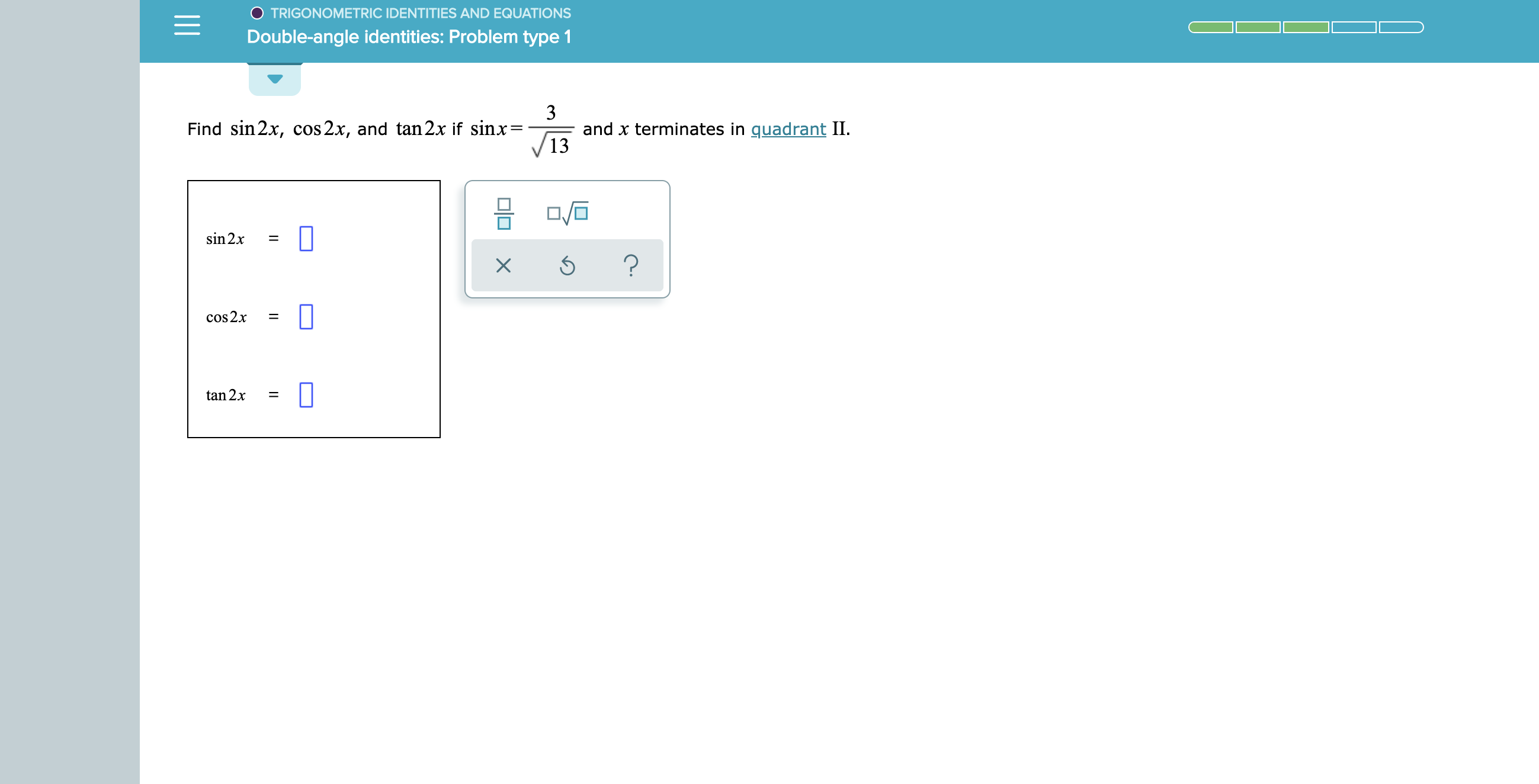


Answered Trigonometric Identities And Equations Bartleby



Using Trigonometric Identities Video Khan Academy



0 件のコメント:
コメントを投稿